3.3 Stein estimation

As discussed at length in Chapter TM:3, an accurate estimate of probability distributions is key to successfull hypotheses testing in general and template matching in particular. Even when coping with the simple case of normally distributed patterns, the estimation of the correct probability distribution parameter from experimentally avaialble data poses some challenges. The key quantity to be estimated in this case is the covariance matrix, which, together with the mean, completely characterize the distribution.

Codelet 4 On covariance estimation errors (R/tm.covarianceImpact.R)
____________________________________________________________________________________________________________

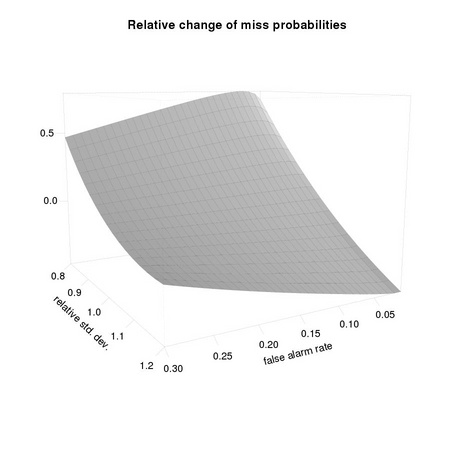
We want to visualize the impact of errors in the estimation of the covariance matrix on P_D, the detection probability, at different operating conditions P_F, as typical in the Neyman-Pearson paradigm. We refer to a single dimensional case, assuming that the distance of class means is 1: the difficulty of the problem is changed by changing the (common) standard deviation σ describing the two distributions. As easily checked from the results of Section TM3.3, we have that σ₀ = σ^-1. We want to compute the impact on P_D(σ₀) given that we set the operating condition using P_F(σ′), where σ′ is our estimate of σ₀ We first need to define a few functions, corresponding to Equation TM:3.15,

1tm.Q <- function(x, sd = 1.0) { 
2  1 - pnorm(x/sd) 
3}

to Equation TM:3.57,

4tm.Pf <- function(nu, sd0 = 1.0) { 
5  tm.Q(nu / sd0 + sd0/2) 
6}

and to Equation TM:3.58,

7tm.Pd <- function(nu, sd0 = 1.0) { 
8  tm.Q(nu / sd0 - sd0/2) 
9}

By choosing σ = 1∕3, from which σ₀ = 3, we get a reasonable testing case:

10tm.covarianceImpact <- function(sigma0 = 3,

We then consider P_F [0.01, 0.3]

11                                pfRange = c(0.01, 0.3, 0.01),

and a moderately large range for σ′ = ασ₀ α [0.8, 1.2]:

12                                pcRange = c(0.8, 1.2, 0.025)) {

We generate the sampling sequences:

13  ats <- seq(-3*sigma0, 3*sigma0, 0.1) 
14  pfs <- do.call(seq, as.list(pfRange)) 
15  pcs <- do.call(seq, as.list(pcRange)) * sigma0

and determine their lengths

16  npfs <- length(pfs) 
17  npcs <- length(pcs)

from which we appropriately size the map:

18  ci <- array(0, dim=c(npfs, npcs))

We now hypothesize several estimated values σ′,

19  for(c in 1:npcs) {

and for each of them, we build the function nu ν = ν(x) : P_F(ν) = x:

20    nu  <- splinefun(tm.Pf(ats, sd0=pcs[c]), ats) 
21    for(f in 1:npfs) {

We can now compute for a selected subset of operating conditions P_F(σ′) based on our estimated standard deviation, the difference in the miss probability with respect to the correct one P_D(σ₀):

22      ci[f,c] <- (1-tm.Pd(nu(pfs[f]), pcs[c])) /(1-tm.Pd(nu(pfs[f]), sigma0))-1 
23    } 
24  } 
25  list(pfs, pcs, ci) 
26}

______________________________________________________________________________________

Figure 3.3: Small errors in the estimation of the parameters of the probability ditributions can have a significant impact on classification performance. The plot shows how the error in the estimation of the standard deviation of normally distributed data results in an amplified detection error.

Figure 3.4: Shrinkage covariance estimation, based on the James-Stein insight, significantly outperforms the ordinary maximum likelihood estimator. The advantage increases with pattern space dimensionality p, and inversely to the number of samples.