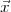 ) for a pattern
) for a pattern 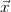 under hypothesis
H0:
under hypothesis
H0:
Fondazione Bruno Kessler - Technologies of Vision
contains material from
Template Matching Techniques in Computer Vision: Theory and Practice
Roberto Brunelli © 2009 John Wiley & Sons, Ltd
A binary classification task can be considered as a binary hypothesis testin problem where one of the
two competing hypotheses H0 and H1 must hold. The two basic probabilities characterizing the
Neyman-Pearson approach to testing are the false alarm error probability PF and the
detection probability PD. The former is the probability of returning H1 when the true world
state is described by H0 and is also known as the probability of a type I error (or false
acceptance rate, FAR). The latter, also known as the test power, gives the probability with
which H1 is returned (by the classifier) when the true world state is H1. Neyman-Pearson
classification, which maximizes PD under a specified bound on PF , results in a simple
thresholding operation on the likelihood ratio value Λ(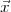 ) for a pattern
) for a pattern 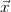 under hypothesis
H0:
under hypothesis
H0:
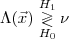 | (3.1) |
The relation between the two probabilities, specifically PD as a function of PF , is usually represented with a receiver operating characteristic (ROC) curve that is extensively discussed in Appendix TM:C:
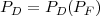 | (3.2) |
The quantity 1 - PD represents the false negative error probability and is also known as the false rejection rate (FRR). The ROC curve is often reported as
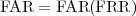 | (3.3) |
While the ROC curve provides detailed information on the trade-off between the two types of errors, classification system are often synthetically characterized by means of the equal error rate (EER), the intersection of the ROC curve with the diagonal
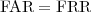 | (3.4) |
When the data distribution under the two competing hypotheses is Gaussian with the same covariance matrix (and different means) the probabilities considered above can be computed in close form (see Section TM:3.3) and the multidimensional case does not present significant differences from the one dimensional one. The key parameter, fixing the maximum achieavable performance, is the separation of the distributions mean with respect to distribution standard deviation. With reference to Equations TM:3.50-58, we can from parameter ν to
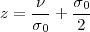 | (3.5) |
in order to compute PD = PD(PF ) exploint the fact that the Q-function is simply the complement to 1 of the distribution function (pnorm)